Learning Teen Numbers in Kindergarten
Teaching teen numbers in kindergarten using a composing and decomposing numbers approach. Students learn the meaning behind place value and catch onto numbers 11-19 quickly.
Here’s a math lesson I taught and the beauty behind letting kinders explore concepts over and over.
Learning teen numbers in kindergarten without just “learning” by rote visualization!

In math, I really feel like we are making great strides and have found the routine and groove for making it all happen! The last three times I met with my math groups our main focus was on answering the question, “Why do teens have a 1?”
“Why do teens have a 1?”
The first day was almost brutal as we started with a discussion and didn’t get very far.
We used some ten frame manipulatives and made some teen numbers to try and find out why, but nothing really seemed to stick by the end of our exploration.
We used a decomposing statement to write down what we made and boy did I make a big deal out of this number one that we saw!

We’ve seen this statement every day since the beginning of school as part of our calendar routine, but now we took our fingers and rainbow slid the number from the statement to the correct place value in the first box.

I don’t want to say that I expected it, but I figured we’d need a few times of hitting this to really get the concept.
Oh boy. Some of them may have appeared more confused than anything.
Would we really be able to learn our teens better by understanding why 13 looks the way it does?
This is my hope. I was holding onto the idea that I could better teach teen numbers in kindergarten by focusing on why the numbers look the way they do.
That way my students could also understand how to compose and decompose 11-19 using groups of tens and ones which is another standard of ours.
Would we really be able to learn our teens better by understanding why 13 looks the way it does?
The second time we met, they looked like deer in the headlights as I re-asked the question, “Why do teens have a 1?”
But would you know it that almost one in each group was able to communicate enough to share that they had gotten it… just when I thought no one had connected the dots.
But, that’s just 1 out of 6 in a group! So, we began exploring again…

Using ten frame foam mats and bingo chips as counters, we made teen numbers and explored numbers larger (depending upon the group) to see why they don’t have a one. Well, this began to grow some excitement. Their eyes lit up in three out of four groups to begin to see that they could form larger numbers in counting by tens and then switching to ones. Using our clapping and snapping they wanted to put their counters and a partner’s counters together. Then they wanted to put them together with another, and then combine them all!
Over the duration of one additional lesson, we had enough time and practice to start small and work up to big numbers (up to 91), all the while writing our decomposing statement as we went that many of them are really figuring it out!
Things are really beginning to click
Things are really beginning to click and they are seeing the why behind this portion of our calendar time in our own math binders, more than just the routine of doing it everyday. So now, they smile when I ask, “Why do teens have a one?” because we are proud to feel like we’ve cracked the code as we are learning more about these numbers!
I am looking forward to the next weeks climbing into December to work on solidifying, working through misconceptions as they come and continuing to excite them about those big numbers and using what they are learning about counting by tens and ones to put it all together!
I share this since its something different I am trying this year instead of first learning what each numeral looks like (I know how much we kinder teachers love 11, 12, 13 and 15 {wink} and then learning how to make it, we are relying on our rote counting and 1:1 counting skills to make it first and then determine why it looks the way it does. By trying it this way we are hitting all of these Common Core Standards:
- K.NBT.1.a Compose numbers from 11-19 from a group of ten ones and additional ones using objects.
- K.NBT.1.b Decompose numbers from 11-19 into a group of 10 ones and additional ones using objects.
- K.CC.3.c. Print numbers from 0-20 when prompted
- K.CC.3.d. Recognize numbers from 11-20 out of sequence.
- K.CC.5.a. Count up to 20 objects that are in an order by answering the question “how many”.
Let me remember this the next time I want to try something new and it feels like I’m trying to herd a group of cats up Mount Sinai… that with a question and guided exploration we can make it click!
If you like what I do here on KindergartenWorks, then be sure to subscribe today. I look forward to sharing ideas with you weekly.
More Math
- Download a free decomposing sheet (as seen above). Great for laminating and using in groups.
- Teach how to draw a ten frame
- Describe 2D shapes
- Exploring Decomposing and Composing Numbers with Equations
- A Decomposition/Composition Sample Lesson Plan
- Decomposing Teen Numbers Game





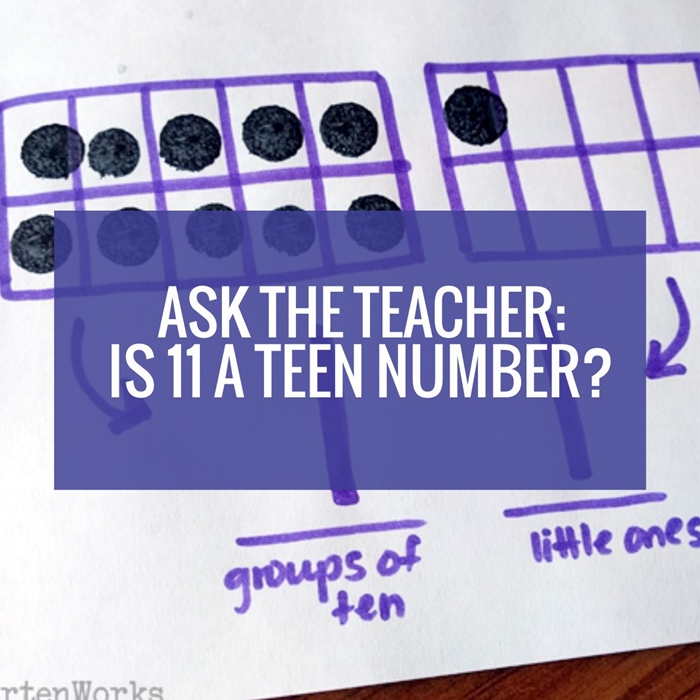


FINALLY!
I have been spent all morning searching online for ways to get kindergartners to understand teen numbers. I found so many blogs and activities, but they all focused on number recognition or just counting. Your post was the first that actually focused on understanding the composition of teen numbers.
Thank you so much for sharing your experience and your ideas!
This is the best compliment – thank you Antoniette!
Are the ten frames above your calendar with the traceable number part of any of your math products?
Hi SP, yes! They are included in our Calendar Pack 😉 Thanks for asking! http://www.teachersnotebook.com/product/KindergartenWorks/calendar-pack-months-weather-labels-book-logs-and-more
– Leslie
This looks amazing and I would love to use it in my classroom, however the downloads don’t seem to work. Any suggestions?
Thank you!
Hi Alyssa,
Perhaps try a different device or web browser. Those tricks might just make downloading the freebies a bit easier. 🙂
– Leslie
This is awesome! Thanks for sharing!!!
Ahh! Thank you!! We can not seem to master teen numbers this year and I am pulling my hair out. Trying this tomorrow! 🙂
Little Miss Glamour Goes to Kindergarten
Thanks Kristin – it definitely took some repeat practice, but not giving up sure did help!
– Leslie
LOVE your blog and ideas. Thanks so much for sharing.
dee [email protected]
Thanks Dee – I greatly appreciate hearing your feedback!
– Leslie
Is the workmat available to download? If so, I’m missing the link.
PS – I LOVE your stuff!
Thanks – take another look at the bottom of the post for the link to the free decomposing sheet. Enjoy!
– Leslie
Thanks for sharing your download. Yeah – this is a tough concept for some kids and I can understand why. Makes it very rewarding when they get it!! Renee
Thanks Renee!
Thank you for the wonderful idea! I cannot wait to try this with my kiddos that are still having a tough time putting it all together!
Erin
[email protected]
Thanks for taking the time to share your thoughts Erin! Hope it really does work for your kiddos too!
– Leslie
This is AWESOME!!!! I have been working on teen numbers and trying to make connections!! LOVE LOVE the download! Another trick in my hat to help get it across– and I too think if they understand WHY WHY then they will be better able to understand the how. Thanks!!
Sarah
[email protected]
Thanks Sarah! Hope the download is a nifty tool for you to help get it across to they why!
– Leslie