Decomposing Numbers – Why We Teach This in Kindergarten
Decomposing numbers means to break down numbers into their sub-parts. Common Core standards has kindergarten students decomposing numbers in two ways.
The first is to decompose numbers into their tens and ones (focus on numbers 11-19) and the second is to show how any number 1-10 can be created using a variety of addends.

I want to focus with you on the NBT.1 Common Core standard which addresses the tens and ones (or place value) aspect of breaking and creating numbers.
Let’s look at:
- how it develops
- how we can practice regularly
- how we extend it for our advanced or accelerated kinders
Since there is so much to cover – I’ve broken it down into three parts. This is part 1 – why would we teach this standard in kindergarten and why do I even talk about it so much on this blog?
Understanding decomposing/composing numbers as teachers
Okay teachers – let’s break it down. There are two main pieces of this standard:
- The first is using objects and words to show that teen numbers have a group of ten and some ones.
- The second is expressing this break down using equations.
When I first came across this standard, I was confused and felt like I truly didn’t understand the value in teaching it. Little did I know what I’d find when teaching it daily in our calendar routine and small group math lessons.

Why do we expect them to decompose and compose numbers?
{And why do I keep writing about it?}
Let’s look long term. The simple answer is because there is value in students being able to see the groupings, relationships and patterns in numbers. We are laying the foundation for students to be able to eventually solve 53+12 and see that they can manipulate it:
50+15
or 60+5
or 50+10+3+2
or any other variety of ways to see the quantity as it makes sense to them.
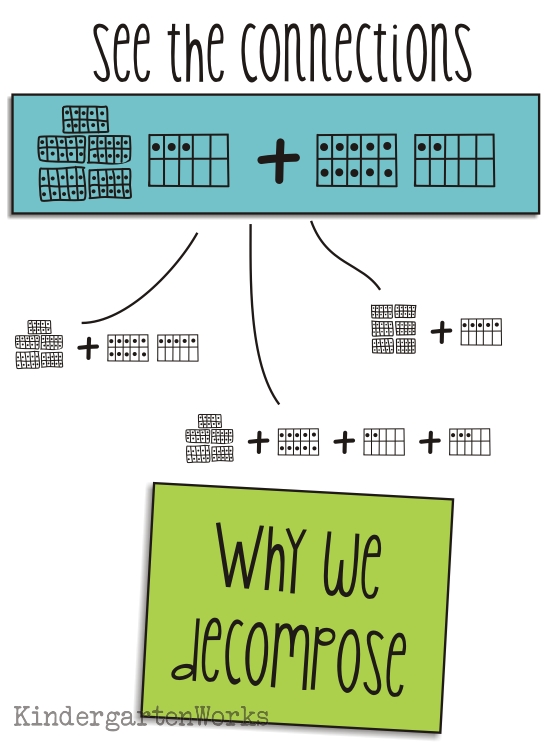
Now that’s the bigger picture and carries us into older grade level Common Core standards… so lets bring it back down to our kindergarten level.
We are working on understanding that numbers 11-19 have a group of ten and then ones.
Seeing numbers broken down into a pattern of their groupings of tens and then the addition of some ones makes these numbers palatable and simple.
Learning how to compose and decompose numbers this way gives them a “visual” {especially if you are representing with ten frames} to what 6, 16 or 67 really looks like and is.
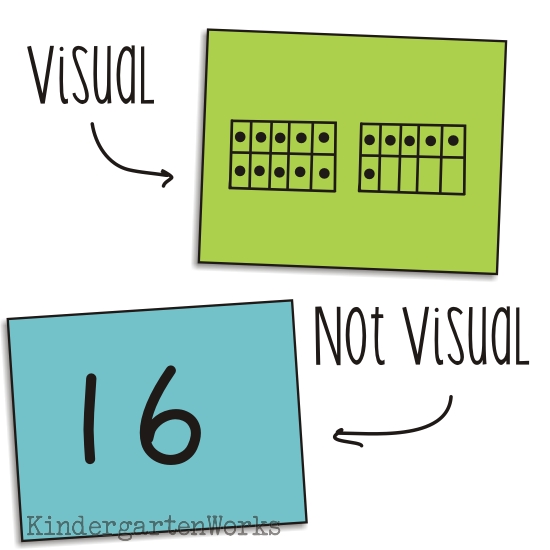
Connecting the visual and the number
The cool thing is that by teaching this foundation of how to compose and decompose numbers 11-19 (and beyond) into their groups of tens and ones – they begin to actually understand why 16 has a one and then a six.
When this clicks, they get so excited that they can’t wait to see if their new understanding applies to “bigger numbers.” And when they begin working on numbers to 99, there is some serious magic that happens.
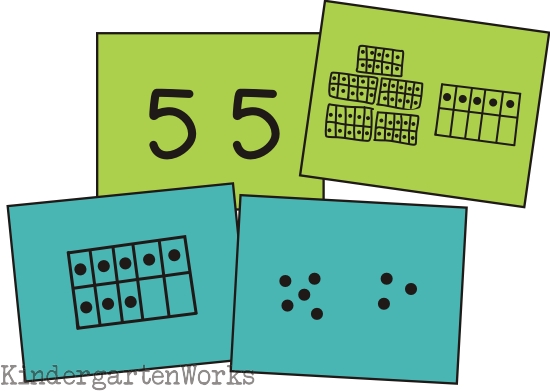
Basically, this standard is huge!
It gives meaning to the number form and totally translates into all other math concepts. I’m not kidding. I’ve never come across a standard (other than counting 1:1) that has so much impact on other standards and is the jumping off point to see kids grow by leaps and bounds in their math skills!
Here are some lesson plans I’ve written about so you can see it in action –
- How to Teach Counting by Tens, Then Adding Ones
- A Sample Decomposing Lesson
- Why Does 10+6=16?
- Learning Decomposing with Words
but don’t forget to read the next post in this series so you can find easy ways to work on this key skill!






![Composing and Decomposing Numbers: What This Looks Like in Kindergarten [3-Part Series]](https://www.kindergartenworks.com/wp-content/uploads/2013/05/Composing-and-Decomposing-Numbers-in-Kindergarten-I-love-the-ideas-in-this-series.jpg)

nice
I was wondering the opposite: how do I open up the concept for students that struggle with counting? How do I extend the introductory lessons for composing numbers? Do I just keep providing them with different ways to compose a number using various manipulatives? How does this help a child who doesn’t understand that we are making a number?
Hi Lupe – if you have kids struggling with counting objects 1:1, then you can do this skill (using a single ten frame) with various manipulatives. The more practice the better. I definitely recommend keeping the range of numbers that you are building very close to their comfort range. Example: If they can only count 5 objects, then work on building 6 and 7 objects in a ten frame so they can begin to see the pattern that 7 is 5 (a whole row filled on top) and 2 more. It’s a starting point!
I have a question? I am a teacher in Ontario, Canada. We work on composing and decomposing numbers to 10 in our curriculum. The idea is that if they know to 10 well then it will relate all the way up. What is your opinion on this?
Hi Jennifer, I think there is a lot of great benefit to composing and decomposing numbers to 10. I think that out of that bunch, knowing what what makes 5 and what makes 10 are the biggest hinging points for kindergarten. They can use that to do more mental math in other grade levels and leads to being able to solve 7+8 by turning it into a 10+5 equation. I think it’s good practice to compose and decompose lots of numbers – including 1-10 – but I saw the most benefit from focusing on subitizing numbers 1-9 (which is still composing/decomposing at an automatic level), seeing them in ten frames and then composing and decomposing 11+ using groups of tens and ones. There are lots of teachers here in the states that focus on composing to 10 as well. I’ve seen lots of worksheets out there on the topic.
– Leslie
Thank you so much for this! I googled & researched many websites but here is where I truly understood how to help my son with his homework. I’m sure I’ll be visiting again soon. 🙂
You’re welcome Julia! I’m so glad you found it helpful. Thanks for letting me know you stopped by.
– Leslie
Hi Leslie! I just wanted to let you know that I blogged about your wonderful ideas for props and re-telling pieces. If you get a moment, check it out at http://sweetkindergartenkiddos.blogspot.com/. Thanks again for the wonderful ideas!
~Kay
Thanks Kay, I appreciate the shout out! Glad you liked the ideas.
– Leslie